What is a $\mathcal{S}$-VAE?

A $\mathcal{S}$-VAE is a variational auto-encoder with a hyperspherical latent space. In our paper we propose to use the von Mises-Fisher (vMF) distribution to achieve this, under which the Uniform distribution on the hypersphere is recovered as a special case. Hence this approach allows for a truly uninformative prior, with a clear advantage for data with a hyperspherical latent representation.

Why use a $\mathcal{S}$-VAE instead of a $\mathcal{N}$-VAE?

VAEs using the Gaussian variational prior/posterior ($\mathcal{N}$-VAE) are the default choice. But although the Gaussian is mathematically convenient, it exhibits some problematic properties both in low and high dimenions; in low dimensions origin gravity takes place, where points are drawn to the origin. In high dimensions, the so called ‘soap-bubble-effect’ is observed, where the vast majority of the probability mass is concentrated on the hyperspherical shell.

Additionally, on a more fundamental level there is the problem of manifold mapping: if the data to be modeled, lies on a latent manifold not homeomorphic to $\mathbb{R}^M$, information is lost. We will show an example of this last phenomenon next.

Example: Recovering a Hyperspherical Latent Structure

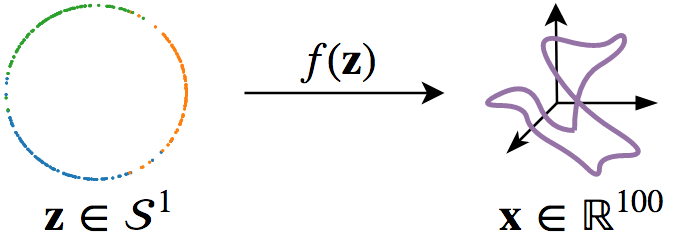
data: We first generate samples from a mixture of three vMFs on the circle, $\mathcal{S}^1$, which subsequently are mapped into the higher dimensional $\mathbb{R}^{100}$ by applying a noisy, non-linear transformation.

models: After this, we in turn train an auto-encoder, a $\mathcal{N}$-VAE, and a $\mathcal{S}$-VAE. We further investigate the behavior of the $\mathcal{N}$-VAE, by training a model using a scaled down KL divergence.

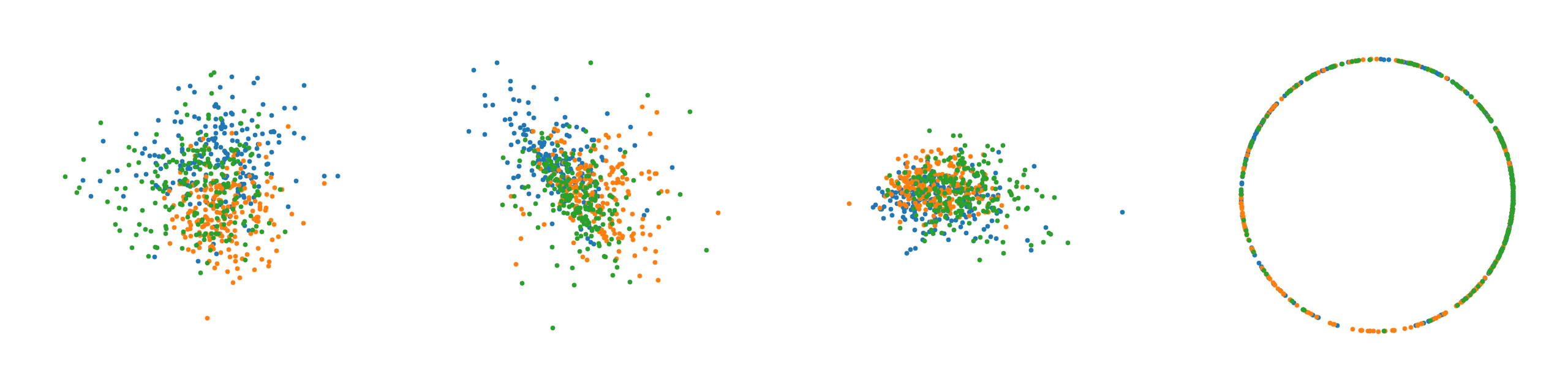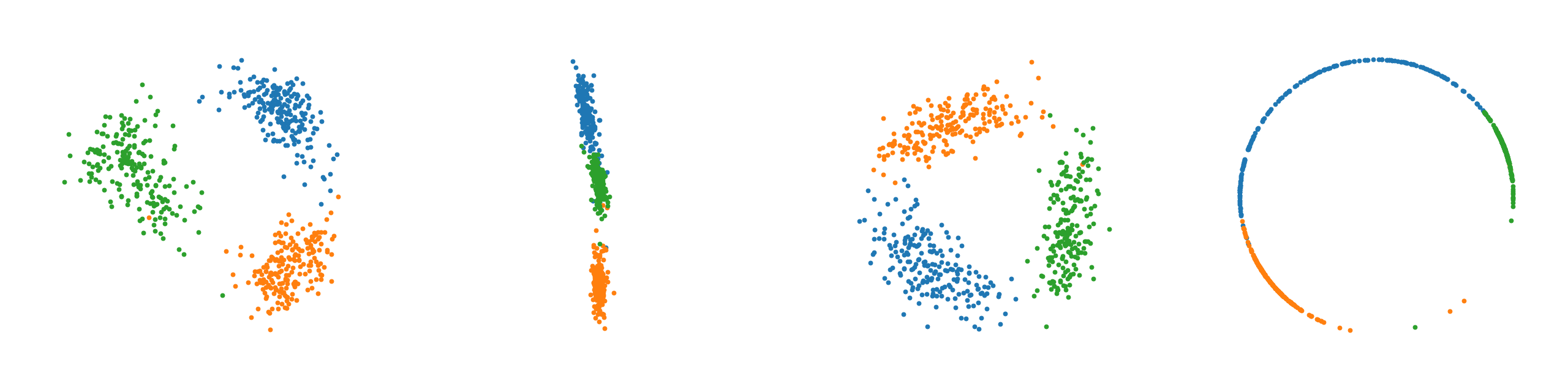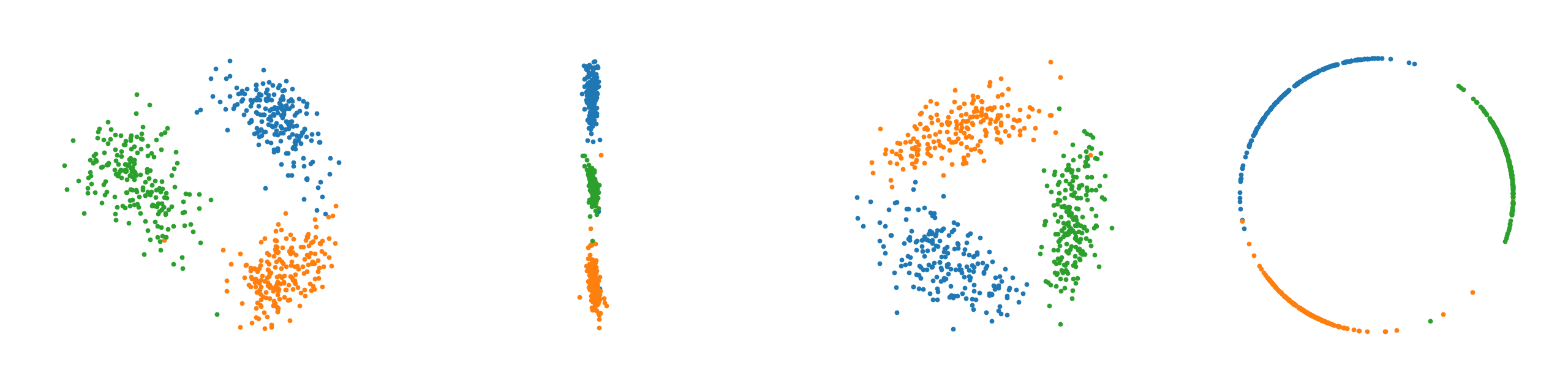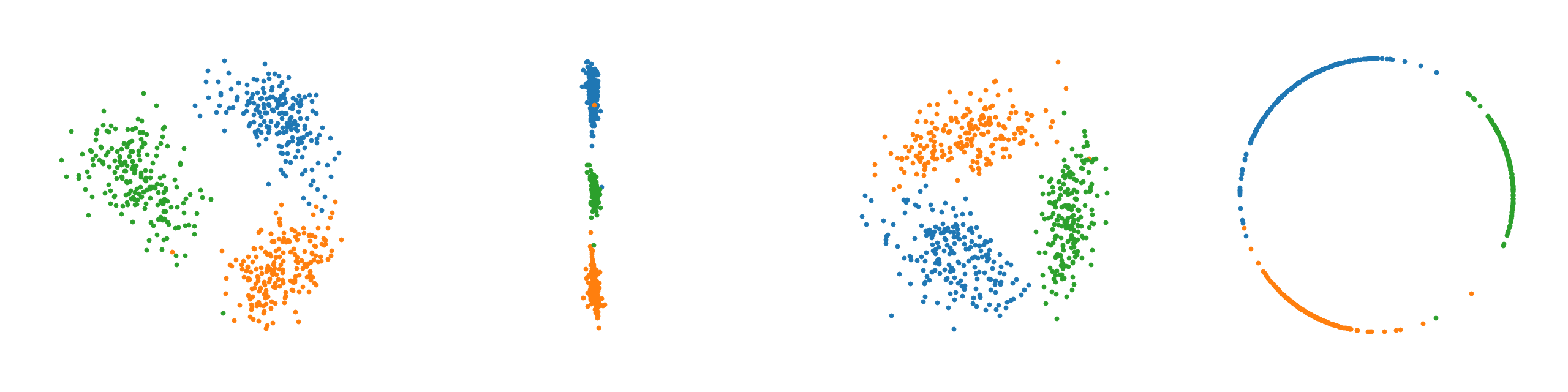
From left to right, plots of learned latent space representations of a. the Auto-Encoder, b. the $\mathcal{N}$-VAE, c. the $\mathcal{N}$-VAE with a scaled down KL divergence, and d. the $\mathcal{S}$-VAE.

Note that as expected the auto-encoder mostly recovers the original circular latent space as there are no distributional restrictions. We clearly observe for the $\mathcal{N}$-VAE that points collapse around the origin due to the KL, which is much less pronounced when the KL contribution is scaled down. Lastly, the $\mathcal{S}$-VAE almost perfectly recovers the original circular latent space. The observed behavior confirms our intuition.

Citation

Davidson, T. R., Falorsi, L., De Cao, N., Kipf, T., and Tomczak,
J. M. (2018). Hyperspherical Variational Auto-Encoders. 34th 
Conference on Uncertainty in Artificial Intelligence (UAI-18).

BibTeX format:

@article{s-vae18,
  title={Hyperspherical Variational Auto-Encoders},
  author={Davidson, Tim R. and
          Falorsi, Luca and 
          De Cao, Nicola and
          Kipf, Thomas and
          Tomczak, Jakub M.},
  journal={34th Conference on Uncertainty in Artificial Intelligence (UAI-18)},
  year={2018}
}